Understanding Marginal Revenue (MR): A Key Concept in Economics [PDF Included]| Definition, Concept, Formula, Product Theory, and Total Revenue

Marginal revenue, a fundamental concept in economics, plays a pivotal role in decision-making for businesses and policymakers alike. It is a concept that lies at the heart of microeconomics, providing crucial insights into pricing strategies, production decisions, and market behavior. By delving into the intricacies of marginal revenue, we can unravel the forces that drive a company’s profit maximization, explore the dynamics of market competition, and even gain a deeper understanding of how public policies impact various industries.

In this article, we will take a comprehensive journey through the concept of marginal revenue, from its definition and importance to its real-world applications. We will break down the concept into simple, easy-to-understand terms, allowing both students of economics and individuals with a general interest in the subject to grasp its significance. So, let’s embark on this exploration of marginal revenue and uncover the economic insights it holds.

Definition and Explanation of Marginal Revenue

Marginal Revenue (MR) is the additional revenue generated by producing and selling one more unit of a good or service. In other words, it represents the change in total revenue that occurs as a result of selling an additional unit of a product.

Marginal revenue is a critical concept in economics, particularly in microeconomics, as it helps businesses and decision-makers determine the optimal level of production and pricing to maximize profits.

Mathematically, the formula for calculating marginal revenue is:

Marginal Revenue (MR) = Change in Total Revenue / Change in Quantity Sold

To put it more simply, if a company sells an additional unit of its product and the total revenue increases by $100, the marginal revenue for that unit is $100. Marginal revenue can vary depending on market conditions, pricing strategies, and demand elasticity, making it an essential tool for businesses to make informed decisions about production levels and pricing.

Understanding marginal revenue is crucial for businesses when setting prices, as it helps them strike a balance between maximizing profit and meeting consumer demand. Additionally, it plays a significant role in economic analysis, particularly in assessing market structures and the behavior of firms within those markets.

Understanding the Marginal Revenue Formula

Marginal Revenue (MR) = Change in Total Revenue / Change in Quantity Sold

Let’s break down the components of this formula:

1. Marginal Revenue (MR): This is what you’re trying to find out. It represents the extra revenue generated by selling one more unit of your product. It’s essentially the additional income from that extra sale.
2. Change in Total Revenue: To calculate MR, you need to determine how your total revenue changes when you sell one more unit. This involves subtracting your total revenue before selling the additional unit from your total revenue after selling it.
3. Change in Quantity Sold: This is simply the quantity of the product you sell before and after adding one more unit to the market.

Now, let’s put the formula into action with an example:

Let’s say you’re selling widgets, and your total revenue from selling 9 widgets is $450. When you sell the 10th widget, your total revenue increases to $520.

First, calculate the change in total revenue: Change in Total Revenue = Total Revenue after 10 widgets – Total Revenue after 9 widgets Change in Total Revenue = $520 – $450 Change in Total Revenue = $70

Next, determine the change in the quantity sold: Change in Quantity Sold = 10 widgets – 9 widgets Change in Quantity Sold = 1 widget

Now, apply the formula: Marginal Revenue (MR) = Change in Total Revenue / Change in Quantity Sold Marginal Revenue (MR) = $70 / 1 widget Marginal Revenue (MR) = $70 per widget

So, in this example, your marginal revenue for selling one more widget is $70. This means that if you sell one more widget, your total revenue will increase by $70. Understanding marginal revenue is essential for businesses to make informed decisions about pricing, production levels, and profit optimization. It helps you find the sweet spot where you maximize your profits by considering how changes in quantity sold impact your revenue.

Marginal Revenue Curve

Total Revenue and Marginal Revenue

Total Revenue (TR) and Marginal Revenue (MR) are two crucial concepts in economics, particularly in microeconomics, that are used to analyze a firm’s revenue generation and make important pricing and production decisions. Let’s explore these concepts in detail.

Total Revenue (TR):

Total Revenue refers to the overall income generated by a firm from selling a certain quantity of goods or services. It is calculated by multiplying the quantity sold (Q) by the price at which the products are sold (P).

Mathematically, TR is represented as:

[TR = P \times Q]

• P represents the price at which each unit is sold.
• Q represents the quantity of units sold.

Total Revenue is a straightforward concept. It provides a measure of how much money a firm earns from its sales at a given price and quantity. However, it doesn’t tell us how revenue changes as output varies, which is where Marginal Revenue comes into play.

Marginal Revenue (MR):

Marginal Revenue, on the other hand, is the additional revenue a firm earns from selling one more unit of its product. In other words, MR is the change in total revenue resulting from selling an additional unit.

Mathematically, MR is represented as:

[MR = \frac{\Delta TR}{\Delta Q}]

• ΔTR represents the change in total revenue.
• ΔQ represents the change in quantity sold.

The key points to understand about MR are:

1. In a perfectly competitive market, where firms are price takers, MR is equal to the market price (P) and remains constant. This is because firms can sell any quantity they desire at the prevailing market price without affecting that price.
2. In markets with imperfect competition, such as monopolistic or oligopolistic markets, MR typically decreases as a firm produces and sells more units. This is because to sell more units, a firm often needs to lower its price, which reduces the revenue generated from each additional unit.

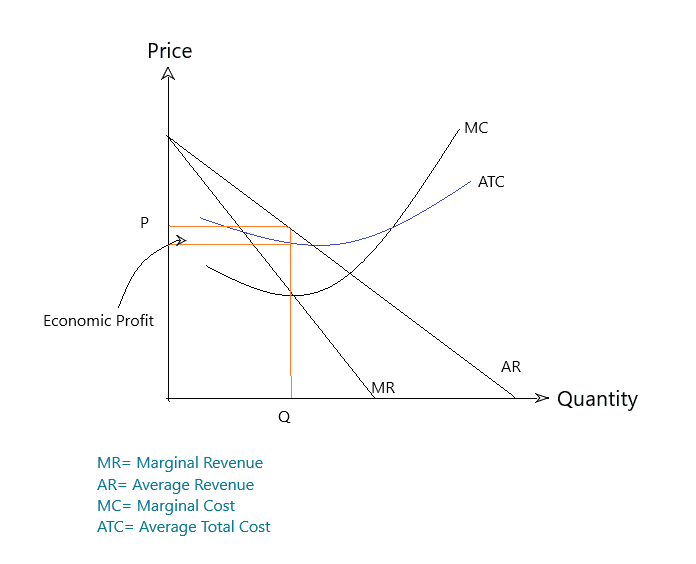
Understanding the relationship between Total Revenue and Marginal Revenue is critical for firms to determine their optimal production levels and pricing strategies. Firms seek to maximize their profit, and this involves producing where MR equals Marginal Cost (MC) since this is where the additional cost of producing one more unit is exactly offset by the additional revenue earned.

In summary, Total Revenue is the total income from selling a specific quantity of products, while Marginal Revenue is the additional income gained from selling one more unit. Both concepts are central to economic decision-making, especially in pricing and production choices for businesses.

Relation Between Marginal Revenue and Product Theory

The relationship between Marginal Revenue (MR) and the theory of production, often referred to as the Theory of Production or Production Function, lies in their intertwined roles in helping firms optimize production, make pricing decisions, and maximize profit. Here’s how these concepts are related:

1. Marginal Revenue (MR):

Marginal Revenue represents the additional revenue a firm earns from selling one more unit of a product. Its key characteristics include:

• MR is dependent on the market structure. In perfectly competitive markets, MR is constant and equal to the market price. In imperfectly competitive markets, MR typically decreases as more units are produced and sold.
• Firms aim to maximize profit by producing at the quantity where MR equals Marginal Cost (MC).

2. Theory of Production:

The Theory of Production is concerned with how firms produce goods and services efficiently and the relationship between inputs and outputs. Key elements include:

• The Production Function, which illustrates how inputs (such as labor and capital) are transformed into output.
• The Law of Diminishing Marginal Returns, which states that as a firm increases one input while holding others constant, there comes a point where each additional unit of input contributes less to the overall output. This law highlights the diminishing marginal returns as additional units of input are added.

The Relationship:

The connection between Marginal Revenue and the Theory of Production becomes apparent in the following ways:

1. Profit Maximization: Firms aim to maximize profit, and MR plays a pivotal role in this process. Profit maximization occurs when MR equals MC. The Theory of Production helps firms understand the relationship between inputs, output, and costs, allowing them to determine the optimal level of production.
2. Input-Output Relationship: The Theory of Production, particularly the concept of diminishing marginal returns, helps firms optimize their input-output relationship. It provides insights into how varying the quantity of inputs influences output. Firms can use this knowledge to minimize costs while maximizing production.
3. Marginal Revenue and Diminishing Marginal Returns: In imperfectly competitive markets, as firms produce more units (output), MR typically decreases. This relationship mirrors the concept of diminishing marginal returns in the Theory of Production. When a firm increases production substantially, it may incur higher costs due to additional inputs, and the additional units sold might yield less revenue due to the need to lower prices to attract more customers.

Download Marginal Revenue PDF

Key Takeaways

1. Definition of MR: Marginal Revenue is the additional revenue a firm generates by selling one more unit of a product. It represents the change in total revenue resulting from selling an additional unit.
2. Market Structure Matters: MR depends on the market structure. In perfectly competitive markets, MR is constant and equal to the market price. In imperfectly competitive markets, MR typically decreases as more units are produced and sold due to the need to lower prices to attract additional customers.
3. Optimizing Profit: Firms seek to maximize profit, which occurs when MR equals Marginal Cost (MC). The point of profit maximization is where the additional cost of producing one more unit is offset by the additional revenue earned.
4. Diminishing Marginal Returns: In production, the concept of diminishing marginal returns is related to MR. As a firm increases one input while keeping others constant, there’s a point where each additional unit of input contributes less to the overall output, leading to diminishing marginal returns.
5. Pricing and Production Decisions: Understanding MR is critical for businesses in determining the optimal level of production and pricing strategies. It helps firms balance revenue and costs to maximize profitability.
6. Marginal Revenue and Total Revenue: MR is closely related to Total Revenue (TR), as TR is the overall income generated by selling a certain quantity of goods at a given price. MR informs how changes in output impact TR and helps firms decide on their production levels and pricing strategies accordingly.
7. MR and Demand Elasticity: Inelastic demand implies that changes in price have a relatively small impact on the quantity demanded. In such cases, raising the price may increase total revenue, and MR may be positive even when the price rises. On the other hand, inelastic demand may lead to negative MR when price is lowered.
8. Decision-Making Tool: MR is a powerful tool for firms to make informed decisions regarding pricing and production. It aids in finding the optimal level of output to maximize profit and adapt to market conditions.
9. Market Competitiveness: MR plays a significant role in assessing market competitiveness. In perfectly competitive markets, firms are price takers, and MR is equal to the market price. In contrast, imperfectly competitive markets allow firms to influence prices by altering their output.
10. Key Element in Economic Analysis: MR is a key element in analyzing market structures, firm behavior, and the impact of public policies on various industries. It’s used to understand how different market structures affect a firm’s pricing and production decisions.